1. Research Project Objectives.

Recent directions of scientific research on modern construction steels are twofold. The first is the development of multiphase microstructures with reasonably smooth gradients of properties. Such materials benefit from the best features due to the mix of phases they are made of. On the other hand, smooth gradients between microstructure constituents improve the local fracture resistance, which is crucial in specific manufacturing processes. The second direction of the research is connected with the models, which are used for particular purposes focused on simulations, which account for the disturbed and noisy measurements of parameters and predict uncertainty of properties of products. Due to noisy measurements, uncertainty propagation plays a pivotal role in simulations of processes. Both directions of research are demanding as far as modelling is considered. Classical deterministic models, characterized by decreasing reliability, should be replaced by stochastic approaches.

The main objective of the project is development of the model describing evolution of steels’ microstructure and phase transformations using stochastic internal variables, which corresponds to both mentioned above fields of study. A suggestion was made in [1] that more balanced properties of multiphase steels can be achieved by tailoring the local gradients of properties in the microstructure. The advanced models are needed to gain knowledge on distributions of microstructural features and to design thermal-mechanical cycles, which will allow obtaining moderate gradients of properties and will result in improved local formability. The limitations of current design methodologies result from limited predictive capabilities of the models, as far as knowledge about distribution of parameters is considered. Moreover, due to the time consuming and costly experiments, often only few technological variants can be compared and the found result may be far from the optimal.

Our objective is to develop a model, which will enable investigation of the correlation between the complex microstructure and mechanical properties of products. We want to prove in our project that description of the evolution of the heterogeneous microstructure of multiphase steels using the stochastic model is possible and it will create a capability to predict gradients of properties. In consequence, it will contribute a new knowledge on evolution of steels’ heterogeneous microstructure and will be a useful tool in optimization of production cycles to obtain more balanced mechanical properties of multiphase steels. It is also assumed that the stochastic model will have capability to predict product properties with certain probability, accounting for the uncertainty of the input from sensors. The reliable, accurate and fast stochastic model should contribute to the efficient design of the hot forming and cooling processes in technological lines.  The low computing cost of the model is crucial in the present project.

The scientific goal of this project is to answer the question to what extent it is possible to predict the heterogeneity of the steel microstructure after cooling based on the stochastic model.  To achieve that goal, we propose a model with internal stochastic variables dedicated for metallurgical industry, predicting evolution of heterogeneous steel microstructure during phase transformations. We will model the process through stochastic differential equations. The coefficients in equations will be either random variables or stochastic processes. Identification of the model coefficients will be performed by the inverse approach with the objective function based on a comparison of measured and calculated histograms of selected parameters of the microstructure. Monte Carlo method will used to solve evolution equations accounting for the random phenomena. Following this, a model describing relation between heterogeneous microstructure and local fracture resistance will be developed. Usually it is achieved using Representative Volume Element (RVE). This solution, however, requires large computing effort. Therefore the Statistically Similar Representative Volume Element (SSRVE) will be generated on the basis of histograms of microstructural parameters calculated by the stochastic model.  SSRVE is a statistical simplification of the RVE and it allows for significant decrease of the computing costs [2]. SSRVE will be subject to deformation and local gradients of properties will be calculated. In consequence, evaluation of the resistance to local fracture will be possible.

Developed model, combined with the hot forming model of [3], will help to understand evolution of heterogeneous microstructures during hot forming and controlled cooling processes. The model will be applicable to predict gradients of properties and to compare local formability of various microstructures. It will be a support for the design of optimal technological parameters. Additionally, the whole model will be applied to simulation of manufacturing cycles accounting for the uncertainty of the process parameters.

2. Significance of the project

Continuous development of various industries is associated with the search for new construction materials that combine high strength with good plastic properties and which allow improvement of the process technology. Steels meet these high requirements and due to their low costs of manufacturing and good recyclability they are now commonly used, in particular by the transportation industry including airplane, automotive and rail transport. The resent research in materials science has shown that there is still a huge potential for improvements of properties of steels by control of heterogeneous microstructures [4]. Dual Phase (DP) steels, which are the leading example of multiphase steels, exhibit an excellent combination of high strength and good global ductility. However, despite its excellent global performance, the local formability of DP steels is often not satisfactory enough and thus it limits application of these steels in many complex geometry components. Contrary, Complex Phase (CP) steels with a more heterogeneous microstructure have superior local formability [5,6]. Typical microstructures of the DP and CP steels are shown in Figure 1.

Figure 1 Typical microstructures of the DP (a) and CP (b) steels [6].

It was suggested in [7] that more balanced mechanical properties of multiphase steels can be achieved by tailoring the microstructure gradients. It is a general opinion that one of the most effective ingredients to design materials with certain desired properties is through the control of their phase transformations and microstructure evolution [8]. Several phase transformation models are described in the literature, see discussion in [9], but these models are deterministic and they do not supply information on distribution of microstructural features. In consequence, these models do not allow to control of heterogeneous microstructures after phase transformations.

It was concluded in [1] that application of stochastic functions to a description of evolution of multiphase microstructures will result in an efficient tool for a design of optimal process parameters. In our previous project [3] we developed the stochastic model, which describes evolution of microstructure during hot forming. It was shown that histograms of the microstructural parameters can be predicted with good accuracy and reliability. However, comparison of the microstructures with regards to local formability and in use properties of products requires models describing the material in the final product, after cooling to the room temperature. It means that there is a need for a stochastic model, which describes phase transformations during cooling and predicts local gradients of properties. Such a model would be a novel approach, which will increase the knowledge about microstructure evolutions and may contribute to development of new steels with advanced properties.

During phase transformations a system in a metastable state must eventually pass into a stable state. This passage, known as the nucleation process, has a random nature, as shown in many publications, eg [10,11,12]. The induction time of the nucleation needed to create a nucleus of thermodynamically stable phase is an important feature of this process. It is understandable that induction time is a random quantity. Therefore, in order to describe nucleation in phase transformations it is necessary to account for its random character. Knowledge of statistics in the study of random phenomena is essential. Development of the model, which describes random phenomena at various stages of the production cycle, is the objective of the project.

Prospective applications of the model are twofold. The first is a support of the design of the optimal processing technologies. The second is connected with the Industry 4.0. Modern industry implements various systems of production processes monitoring and data gathering, which work in real time. Therefore, nowadays the models are also used for specific purposes focused on predictive maintenance and assessment of the quality of manufactured elements. Due to noisy and disturbed measurements in the industrial processes uncertainty propagation plays a pivotal role in modelling of these processes. In such a demanding case classical deterministic models have to be replaced by stochastic approaches. The model developed in the project will meet these requirements and will be able to predict properties of product with certain probability accounting for the uncertainty of the input from sensors. In this case the coefficients in the equations will be treated as random fields, see description of the WP2.

3. Concept of the research and work plan.

To prove the main hypothesis of the project the general objective was proposed as development of the phase transformations model for the stochastic independent variables. However, to prove this hypothesis convincingly the whole manufacturing cycle composed of microstructure evolution during hot deformation and phase transformations during cooling have to be considered. Stochastic model of the microstructure evolution during hot forming was developed in our earlier project [3] and it is a starting point for our current research. This model of [3] is based on the Kocks, Estrin and Mecking (KEM) model [13,14] and additionally accounts for the random character of the recrystallization and predicts distribution of the two internal variables: dislocation density and grain size. The main equation of the model is [15]:

  (1)

where: t - time, – strain rate.

Coefficients A₁ and A2 responsible for hardening and recovery are defined in Table 1, where: b – a module of the Burgers vector, Z – Zener Hollomon parameter, l – average free path for dislocations, T – temperature in K, R – universal gas constant, a₁, a₂, a₃, a₉, a₁₀ – coefficients.

Table 1. Relationships describing coefficients in equation (1).

Hardening	where:
Recovery

 

The parameter (t_i), accounts for a random character of the recrystallization and its distribution is described by the conditions:

  (2)

In equations (1) p(t_i) is a function, which bounds together the probability that the material point recrystallizes in a current time step and present state of material:

 (3)

D – grain size,  – energy per unit dislocation length, a₄, a₅, a₆ – coefficients.

Since the function in (3) is possibly unbounded, it was truncated at value 1 in (1). In equation (3) coefficient  represents a mobile fraction of the recrystallized grain boundary and depends on (already known) distribution of (t_i-1) in previous step:

 (4)

where: a₈ – coefficient, q - a small number representing a nucleus of a recrystallized grain, which is added to avoid zero value of (t_i) in the case P[(t_i-1)=0] = 0.

Numerical solution of equation (1) was performed in the project [3] and is described in details in publications [15,16]. Flow chart of the model is presented in Figure 2. It has to be emphasized, however, that analysis of properties of products and their resistance to local fracture requires simulation of phase transformations and development of the model, which correlates microstructural features with properties. Development of such model is the main objective of the project.

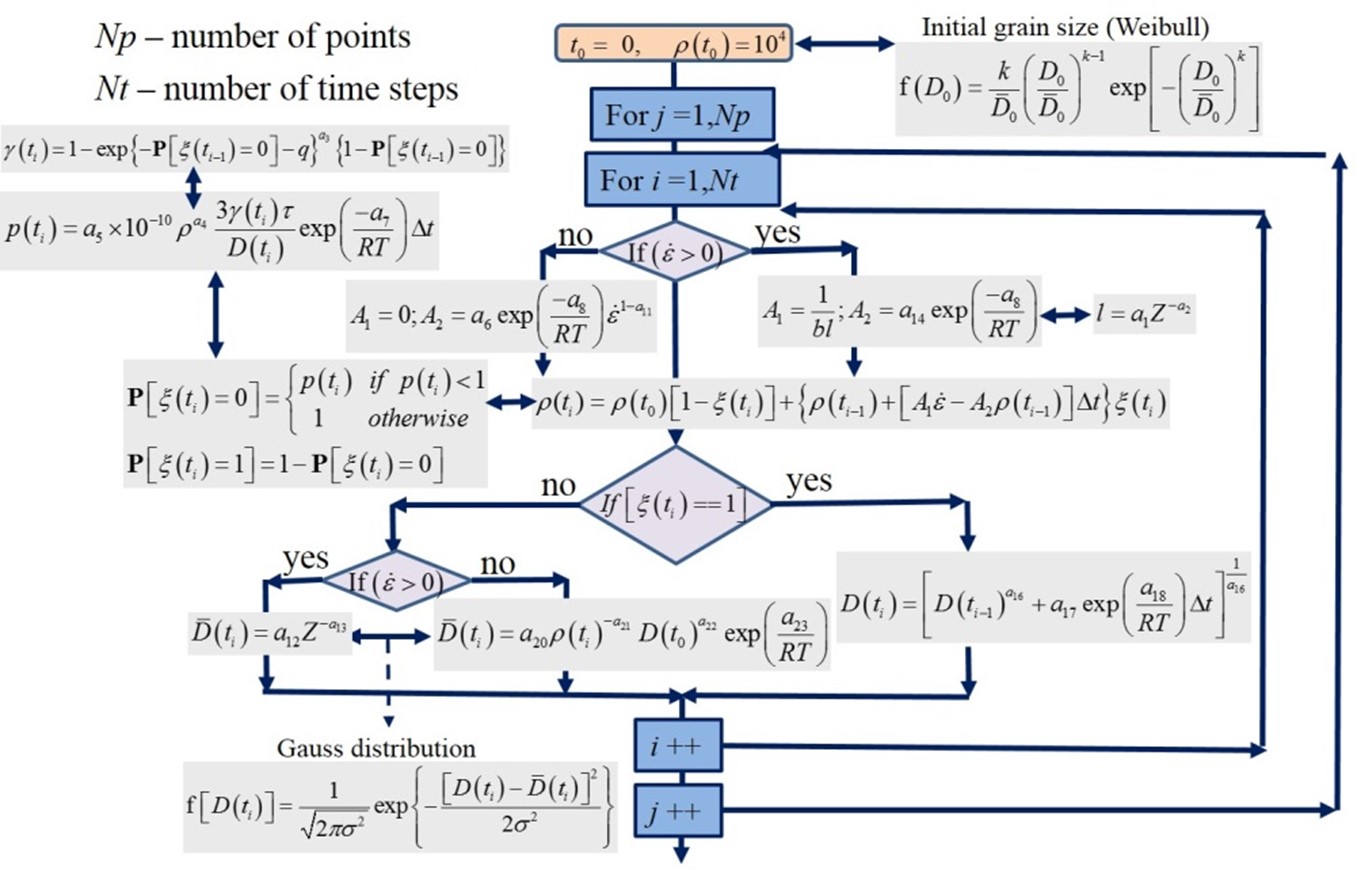
Figure 2 The flow of calculations in the stochastic model of microstructure evolution developed in [3].

Our present project is focused on phase transformations during cooling after hot forming. Existing phase transformation models are deterministic and are not capable to predict distributions of microstructural features. Having the results of the hot deformation model [3] in the form of histograms, we will develop in the current project a new stochastic model of phase transformations, which will account for random character of some phenomena. The objective will be achieved by adaptation of the existing phase transformation models based on the differential equations to stochastic independent variables. An upgrade of the Leblond model [17] will be used to describe kinetics of phase transformations. This model is based on the differential equation with respect to time and it does not need an application of the additivity rule when the temperature varies during the process. It is the main advantage of this approach. The original Leblond model [17] assumes that the rate of the transformation is proportional to the distance from the thermodynamic equilibrium in a given temperature:

  (5)

where: t – time, X – volume fraction of a new phase, X_eq – equilibrium volume fraction of the new phase in the temperature T, k – material constant.

An upgrade of the Leblond model is described in [18]. Since experiments show that a response of the material to the changes of the temperature is similar to the second order inertia term, the second order differential equation was proposed:

  (6)

where: B₁, B₂ – coefficients, which are functions of the temperature, which in turn depends on time. In more general approach, which should model the process in a better way, these coefficients will be random variables (stationary stochastic process) or more general stochastic processes. Such random ordinary differential equations often appear in natural sciences and engineering, eg. [19,20,21].

Then it is planned to conduct analysis of the obtained equations. As the first step we will look for possible simplifications in order to find exact, analytical solution for constant temperature or constant cooling rate. Analysis of the stability of the solution depending on the equation coefficients will be performed while these coefficients are defined as stochastic processes or random fields. This knowledge will be used as a benchmark in numerical simulations. We will also try, where possible, to determine mathematically strict conditions which ensure existence and uniqueness of the solution.

Moreover, the coefficients B₁ and B₂ in equation (6) depend on the state of the material prior to phase transformations. In our case this state will be described by two internal variables: dislocation density and grain size. Both variables are stochastic and will be calculated using the solution of equation (1) developed in the project [3]. Typical distributions of the dislocation density during and after the deformation are shown in Figure 3a. Histograms of the grain size were also calculated and the results were compared with the experimental data, see Figure 3b where grain size in 2 s after the end of deformation is presented (strain 0.2, temperature 1000^oC).

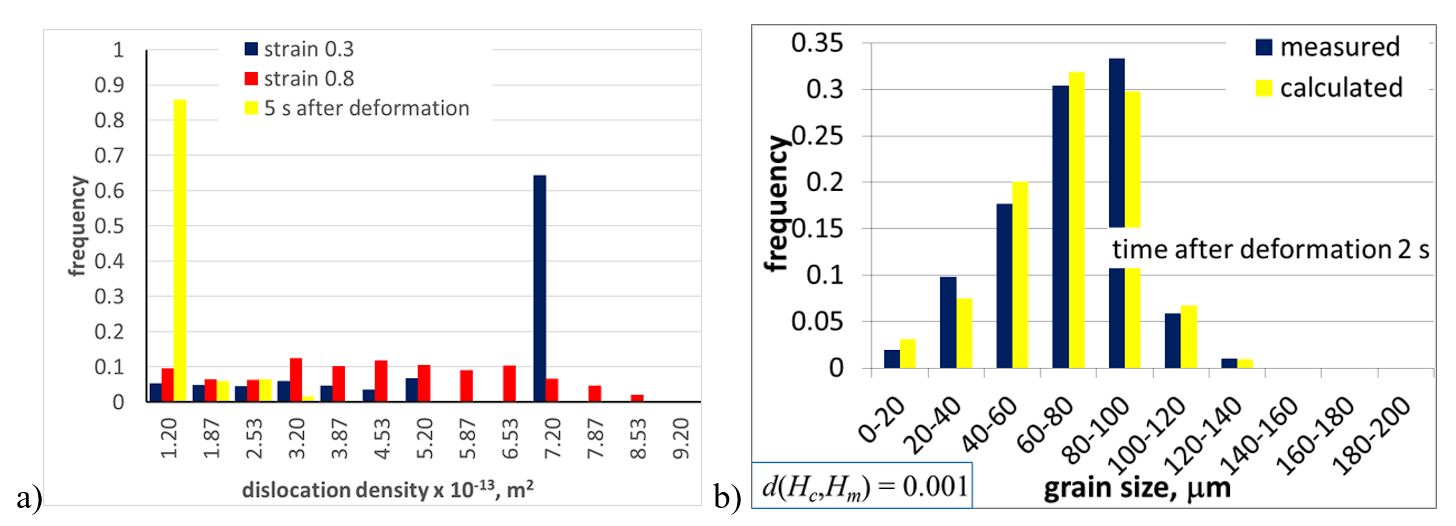
Figure 3 Selected examples of histograms for the dislocation density (a) and grain size (b) during and after the hot deformation calculated using the model developed in [3].

Phase transformation model preceded by developed earlier hot deformation model will be capable to simulate the whole manufacturing cycle composed of hot forming and controlled cooling, which is schematically shown in Figure 4.  Phase transformations introduce additional stochastic element in the model connected with the random character of the nucleation of the new phase. As it has been mentioned above, the problem of the random character of the nucleation is discussed in several publications, eg. [10,11,12]. However, majority of published papers deal with crystallization during solidification [10] or precipitation [22] or various deposition processes [11]. To the best of the Authors knowledge, research on stochastic modelling of nucleation during phase transformation in steels is scarce. We intend to develop such model based on stochastic processes. Starting point will be random variables which resulting from random nature of dislocation density and grain size (Figure 3). Fitting the plots in this figure by skewed distributions will be one of the goals. Inverse analysis will be applied to describe most appropriate distributions, which will be further used as main building blocks of coefficients of equation (6). The deterministic dependence of B₁ and B₂ on  and D will be used.  In later, we will include other factors which will lead to more complicated stochastic processes.

In the first approach we will perform solution assuming Poissonian homogenous nucleation. The statistical approach will be based on the fundamental knowledge regarding nucleation [23,24]. The deterministic nucleation rate equation will be substituted by the probability that the nucleus of the new phase occurs in the time t:

  (7)

In equations (7) p(t_i) is a function, which bounds together the probability that the material point becomes a nucleus in a current time step and present state of material. This probability will be based on the following knowledge about nucleation sites:

• 1) nucleation rate increases with an increase of the undercooling below Ae3 temperature,
• 2) grain boundaries and shear bands in the deformed microstructure are the privileged locations of nuclei.

On the basis of these assumptions, the following equation will be considered as the first step:

  (8)

D – grain size,  – energy per unit dislocation length, b₁, b₂, b₃, b₄ – coefficients.

In equation (8) grain size and dislocation density are stochastic variables, which will be calculated by the model developed in [3], see example in Figure 3.  Coefficient b₁, b₂, b₃, b₄ will be determined by the inverse analysis for the experimental data, see description of the WP4.

Differently from Poissonian nucleation, the more realistic formulation makes use of actual nucleation rate. Thus, the main objective in the project will be to apply statistical solution to account for the time dependent non-Poissonian heterogeneous nucleation, as an opposite to homogeneous and isotropic one, which is still commonly assumed in modelling. In the non-Poissonian approach the conventional model of the nucleation rate will be adapted to a random process by considering a random distribution of circular or spherical nuclei [11,25]. The differential-critical-region method will be used. The kinetic equation for the probability that a point in space, chosen at random, is transformed in an infinitesimal interval of time dt. In the following, two nucleation rates will be considered, namely: i) the “phantom included” nucleation rate, I₀(t ), i.e., the nucleation takes place throughout the entire space independently of whether the nucleation point has been already transformed or not, ii) the “actual” nucleation rate, I_a(t ), for which the nucleation in the untransformed phase only is considered. The relationship between the two nucleation rates reads I_a(t ) = I₀(t)[1 – ξ(t)], where 0 < ξ(t ) < 1 is the probability that a point in space, taken at random, becomes a nuclei at t.

The solution of kinetics equations of phase transformations for distribution functions should maintain low computing costs characteristic for the mean field models. On the other hand, information about distributions of such parameters as ferrite grain size, volume fractions and size of hard constituents will become available. Thus, the objective of the project is to develop models based on the distribution functions (stochastic models), which will combine simplicity of the mean field models and predictive capabilities of the full field approach.

Attempts of solving nucleation equations (7) and growth equations (5) or (6) using numerical methods (e.g. Monte Carlo) will be considered. In particular, algorithms developed in [20,26] for approximation of solutions of random differential equations will be used in the case when B₁ and B₂ are random variables or stochastic processes. Therefore, particular objective of this part of the research is, first of all, finding distributions describing  and D at the end of hot deformation, which is starting point for (5) and (6). Since equation (6) in the final form will have stochastic parameters, we foreseen need of using advanced numerical methods for differential equations. The whole description above is dedicated to ferritic transformation, but similar models for the pearlitic and bainitic transformations will be developed. The flow of calculations is presented in Figure 4b.

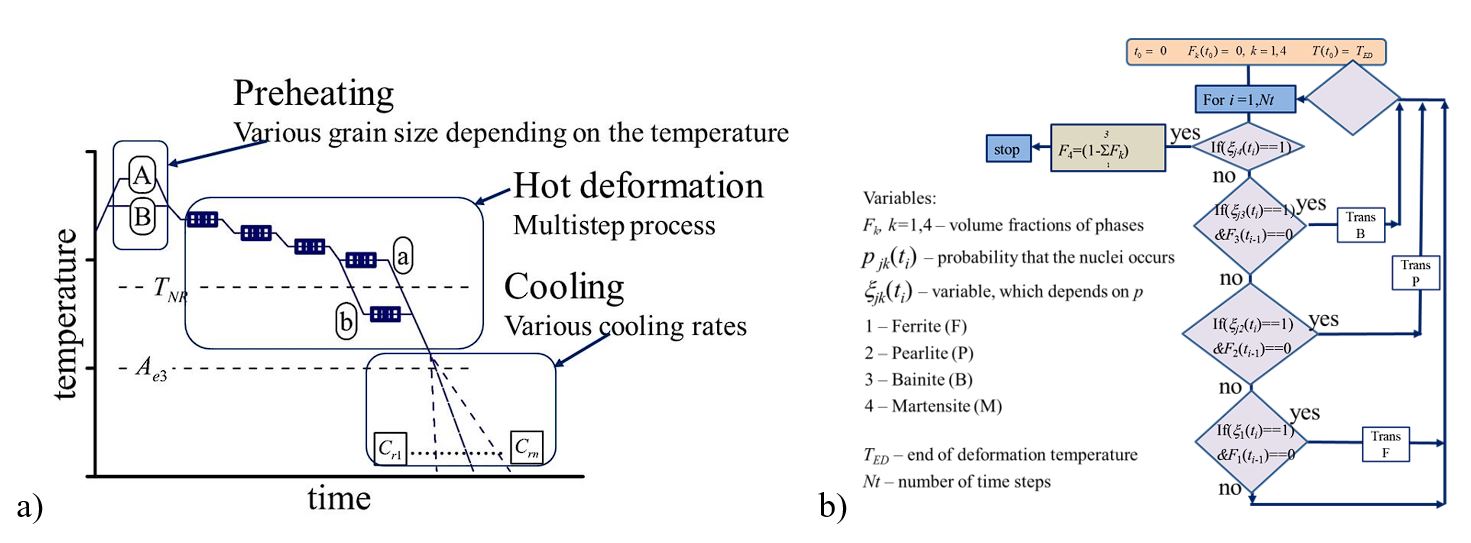
Figure 4 Schematic illustration of the manufacturing cycle composed of hot forming and controlled cooling (a) and flow of calculations for the model covering 4 transformations (b).

Application of the developed stochastic model to real materials and processes would require the identification of model coefficients. The problem of coefficients identification in material models is well known and widely discussed in the literature as an inverse problem [27]. The stochastic model contains vector of coefficients a, which become design variables in the inverse analysis.

A mathematical formulation of any material model or material processing model is a direct problem. Let K: X  Y be a mapping between two normed spaces X and Y:

  (9)

The mapping K describes a process under study. Vector x contains two sets of parameters, coefficients in the model a and process parameters p, x  = {a,p}.

In the case of material processing, the first quantity includes material model coefficients and the latter includes parameters describing the process conditions. Strain rate during deformation and temperature during the whole process are the most common parameters.  Two problems can be defined for the operator K [9]:

• 1) a direct problem: for known x, evaluate y = Kx,
• 2) an inverse problem: for known y, solve the equation for x.

In the case of the thermomechanical processing problems, which are considered in the present project, two classes of inverse problems are distinguished (Figure 5):

• 1) an identification problem: estimation of quantities a characterising a material,
• 2) a reconstruction problem: determination of process parameters p for the known coefficients a.

Both cases will be considered. The problem of reconstruction, which allows finding process parameters giving required output, is known as process optimisation [28] and will be the objective of the WP7.

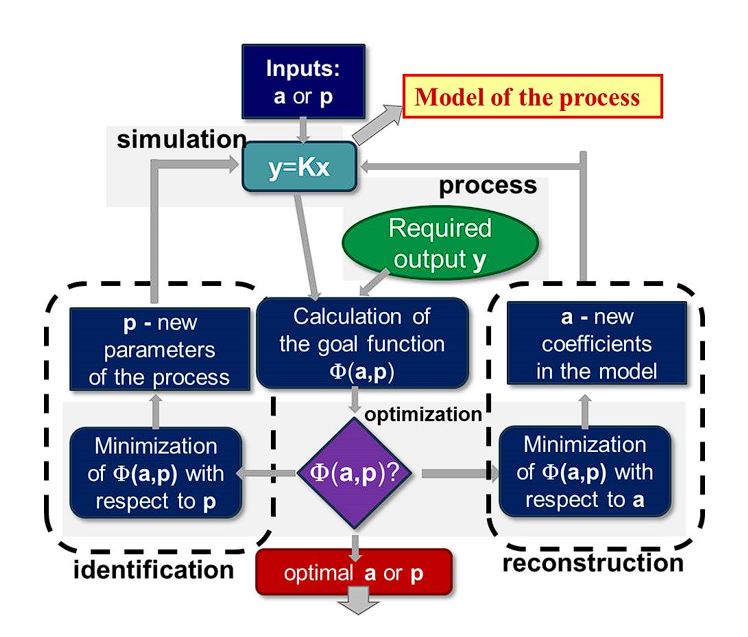
Figure 5 Flow chart of the inverse algorithm used in identification of the stochastic model parameters (left side) and in the reconstruction problem (right side).

To solve a physical problem, its mathematical model must be well-posed, which means that a solution to the problem exists, it is unique and it continuously depends on the data (the stability property). If there is more than one solution, additional, more restriction conditions must be included in the model. Since in the case of thermomechanical processing of metallic materials the material models are nonlinear, the inverse problem is transformed into an optimisation task, as shown in Figure 5.  The optimal parameters are determined by searching for a minimum of the following objective function:

  (10)

where: y_c – outputs calculated for model coefficients a and process parameters p, y_m – measurements in the experimental tests with process parameters p (for identification task) or required output of the technological process (for reconstruction task), d – metric in the output space.

However, the classical inverse problems do not take into account stochastic models and the random parameters, corresponding to the recrystallization and nucleation during phase transformations. Therefore, we redefined the classical inverse approach described in [9,27] for a stochastic variable material model. The statistical inverse problem for the identification of a non-Gaussian tensor-valued random field in high stochastic dimension will be formulated in the present project. Definition of model output in the form of histograms is necessary to solve this problem. Thus, considering the stochastic nature of the process, it will be necessary to compare the model outputs for particular sets of coefficients, taking into account that the random factors in the model. We have analysed and compared various measures of the distance between histograms [15] and the Bhattacharyya distance measure [29,30] was selected as ensuring the fastest convergence in the optimization. Let us recall, that Bhattacharyya distance between histograms H₁ and H₂ is defined as:

  (11)

where: n – number of bins and:

  (12)

Based on the calculated probabilities, the distribution of stochastic variable will be compared with obtained histogram, and to estimate and compare a probability density function, norm in L¹ will be applied.

Optimization of the objective function (10) will be performed in the WP4. The Authors have been for many years involved in research on application of the optimization methods in processing of metals [28,31].  One observation we have made during previous research on the inverse analysis was that the arbitrary choice of starting values or population of the coefficients in the nonlinear problems does not guarantee the best and unique solution. Considering that no physical bounds have been established for some of the material constants of the model, the task of finding the best solution can be tedious and present a source of uncertainty [32,33]. To address this challenging task we will propose dividing the procedure between subsequent phase transformations while holding the other transformations fixed, and monitored the goal function improvement by checking the maximum and average residual. We will tune the coefficients in each attempt until a satisfactory convergence was obtained. However, that fitting approach is tedious, nonphysical, and relies heavily on the numerical aspects of the optimization method. At the end, all coefficients can be optimized simultaneously with experimental data at different temperatures and cooling rates with no physical interpretation of the fitting procedure. We expect that it will allow finding more reliable, in terms of uncertainty, solution. The same optimization procedure will be applied in the reconstruction problem in the WP7.

Simplification of the computational domain will be the next objective of the project. Representative Volume Element (RVE) will be designed on the basis of pictures of the multiphase microstructures (see image analysis procedure described in [2], section 5.1) and it will be substituted by the Statistically Similar Representative Volume Element (SSRVE). Authors have an experience in designing SSRVE for the two phase materials (DP steels) [2]. Development of the methodology for design of the SSRVE for multiphase materials (CP steels) will be the goal of the WP5. New criteria, such as contact of phases, length of the boundary between selected phases and stochastic information about phase composition will be added to the typical objective function based on the shape coefficients. When designed, SSRVE will be subjected to plastic deformation and correlation between microstructure represented by histograms and product properties will be determined.

Next objectives of the project will be reached in the WP7 and the WP8. Developed model, connected with the model of [3], will be applied to optimization of production cycles composed of hot deformation and controlled cooling. Processes of laminar cooling after hot rolling and continuous annealing after cold rolling will be considered. The same optimization methods, which are describe above in the context of the inverse analysis, will be used here in the design of optimal technological parameters (WP7). Finally, the developed model will be applied to predict uncertainty of simulation of phase compositions and product properties caused by the noisy and disturbed measurements of technological parameters. In this solution uncertainty of the temperature measurements during the process will be accounted for.

Thus, the global scientific goals of the project are focused on extending the model of [3] to phase transformations and on expanding computational capabilities in material modelling, in order to predict advanced microstructure parameters and final product properties. One of our objectives will be formulating equation (6) in the stochastic form with parameters B₁, B₂ following skew normal (or other, appropriate) distributions (WP1, WP2 and WP3). Since (6) in general form does not have known analytical solutions, and we also add stochastic ingredient in the parameters, the only possible method of solving (6) is by numerical methods. We will start with simpler versions of coefficients B₁, B₂ and assume constant temperature T (isothermal phase transformations). This will be a testing ground for different numerical methods (discretization), when searching for the most accurate method. After choice of most promising numerical methods we will find (numerical) descriptions of the evolution of distributions of parameters of the material, when these parameters change in time as an effect of applied metal forming (continuous change of temperature T in time and other model parameters). Next step in WP4 would be to solve the inverse problem, where by knowing the desired distribution of the solution, one would be able to back-calculate the required parameters. Following this, it is planned in WP6 to compare the obtained results with the experimental data. That would ensure that the proposed approach is meaningful. The final objectives connected with, applications of the model are twofold. The first is the design of the thermomechanical cycles using optimization method, which will be done in the WP7. The second application of the model in the WP8 will be connected with evaluation of the uncertainty of product properties caused by uncertainty of the temperature measurements in the selected industrial process.  Our industrial partner in other project will supply realistic data concerning uncertainty of temperature sensors. Monte Carlo method will be used to solve evolution equation and to calculate product properties.

We expect to reach general objective of the proposed research, which is creation of the possibility for developing effective methodology for design of materials processing, based on the phase transformation model which uses stochastic internal variables. Stochastic methods for material virtual representation have been intensively developed in recent years. These methods form a potentially powerful tool that should allow designing new material technologies. The new contribution of our project is composed in the capability of the proposed model to predict gradients of properties, which are crucial in materials resistance to local fracture. It is also expected that modern numerical methods will offer possibilities of effective solving of evolution equations for stochastic variables. As a consequence, the model much faster than full field models and with larger predictive capabilities than conventional mean field models should be obtained. The model will make predictions of gradients of properties in final products possible and it will become an efficient tool for the design of manufacturing of new generation multiphase steels.

Recapitulating, development of modern numerical tools for detailed and fast numerical simulations of thermo-mechanical processing of multiphase steels will be carried out using four main steps. The first is solution of equations describing evolution of microstructural parameters and phase transformations for stochastic variables. The second will be identification of the model by the inverse solution for the measured histograms of selected microstructural parameters and testing of the developed model. The third goal is development of the relation between heterogeneous microstructures and product properties, in particular resistance to fracture. Finally, allocation of the developed model to optimization of technological parameters and to prediction of the uncertainty of product properties will be the last step of the project. From the practical point of view, these objectives are very important. As we have mentioned earlier, development of modern steels is directly related to control of gradients of properties in the microstructure. Advanced stochastic model proposed in the project should predict distribution of the microstructural features as a function of the technological process parameters.

The main risk of the project is that we may experience problems finding appropriate class of distribution functions reflecting histograms. It may also happen that stochastic nature of (6) will lead to not satisfactory results compared to real world data. Possible solutions, if such case appears, is using nonstandard distribution functions. If problems with model fitting appear, we will invest more time on that problem, and limit other simulations and works beyond that point. Let us stress the fact, that if we do not receive completely satisfactory results of inverse analysis, still theoretical knowledge on phase transformations during cooling will be widely enriched. We strongly believe that our equation (6) goes much beyond what is known on the process under investigation.

In the identification part, an inverse analysis introduces a risk that a unique solution will not be obtained. To solve this problem we will try to narrow a space of optimized coefficients. Too large error (distance between measured and calculated histograms and densities) is another risk in the identification.  In this case we will apply other, more complex optimization algorithms or redefine the objective function. All these risks will enrich knowledge on inverse analysis for models with stochastic character.

The project is divided into eight work packages, which are described briefly below.

WP 1. Development of the mean field statistical models of phase transformations.

The stochastic model, which is the objective of the project, will be general and applicable to any multiphase steel. One typical steel multiphase will be selected as a case study. Authors have an experience in conventional modelling phase transformations and various models, as well as identification methods which will be used in the project, are described in the book [9]. Following this, various methods of development of statistical descriptors of heterogeneous microstructure will be analysed. Numerical tests including sensitivity analysis will be performed. The main steps in this task include:

Creation of physical basis for building a statistical models of multiphase microstructures and for development of advanced set of differential equations describing nucleation and growth of a new phase and evolution of distribution of crucial parameters in time.

Differential equations describing phase transformations using statistical independent variables will be formulated. Descriptors for the following three stages of manufacturing cycle will be selected: i) Initial microstructure before processing, ii) Microstructure evolution and segregation of elements during thermomechanical processing, iii) Microstructure of final products.

Equation (1), which describes evolution of dislocation populations, will be used to simulate microstructure during hot forming. Detailed analysis of the Monte Carlo solution of this equation with the mathematical background was performed in the Authors’ earlier project [3] and is described in publications [15,16,34]. Calculated histograms of the dislocation density and grain size after hot forming will be starting point for modelling phase transformations in the present project.

An upgrade of the Leblond model [17], which is based on the differential equation, will be used to describe kinetics of phase transformations. An upgrade of the Leblond model based on equation (6) [18] will be considered next. We will start with ordinary differential equation, however as explained before, we will transform it to an equation with stochastic parameters.

WP 2. Mathematical background for the phase transformation stochastic model.

We will develop theoretical background for equation (6). First of all, we will look for density functions that can properly describe distribution of dislocation density and grain size. From previous experiments we have identified coefficients generating histograms of these parameters, however continuous functions describing densities are not yet revealed. It will be out first objective. These distributions will be a starting point for distributions of coefficients B₁ and B₂ in (6). We will use them for creation of time dependent equation (6) with B₁ and B₂ being stochastic processes. Our starting point will be stationary process, or even ordinary differential equation where random is only initial point. Our goal, however, will be creation of a model which depends not only on time but also on the whole probability space. We will look for mathematical formulas that may describe nucleation in reliable way. It was observed in practice, that nucleation depends on the whole material, not only on its local behaviour. In this task we will develop mathematical form of coefficients in (6) ensuring the above assumptions. We will also aim at developing formulas for probabilities that are not dependent on time step. Summing up, the aim of this stage are extensive studies on possible forms of equation (6), developing at the same time tools that can be used in further steps of the project. The proposed structure of (6) and distance functions should lead to effective:

• 1) Analysis of the solutions of equations (5) and (6) for B₁ and B₂ independent and dependent on temperature (and thus time)
• 2) Formulation of the inverse problem for the stochastic model and its analysis in various settings
• 3) Formulation of the optimization task for application to the inverse problem and reconstruction problem.

WP 3. Numerical approximation of the stochastic model.

We treat equation (6) as ordinary differential equation with random coefficients. We consider the following three cases: i) B₁ and B₂ are random variables (independent of time), ii) B₁ and B₂ are stochastic processes, iii) B₁ and B₂ are random fields that depend on time and initial value, which also might be of random nature. In each case, for approximation of such random ordinary differential equations (RODEs) with random coefficients we implement algorithms of high accuracy that are based on Taylor expansion and were developed in [20,26]. Such algorithms provide efficient numerical schemes for mean-square approximation of trajectories of solutions of the underlying equations.  We will also provide Monte Carlo simulation of the laws of solutions of underlying RODEs at fixed time points. We provide suitable modification of the known algorithms if needed. For the implementation we plan to use Python/Mathematica. We are going to test efficiency of the used algorithms by conducting numerical simulations in the case when analytic solution of (6) is known  and also in the more demanding case when coefficients of (6) are of complex nature (for example, when B₁ and B₂ are stochastic processes) and analytic solution is not known.

WP 4. Identification of the coefficients in the model.

Identification of model parameters will be performed on the basis of experimental data. Inverse approach will be applied. Since analytical determination of the inverse model is not possible, identification will be transferred into the optimization task. The optimization will be preceded by the sensitivity analysis (SA), which is the field of knowledge investigating the model (mathematical and physical description of the phenomenon under study) behaviour for various input data and model parameters [32]. It determines how the variations of input data and parameters are distributed on the variations of model outputs and influence them. A good practice of the numerical modelling is to identify properly the model coefficients and the SA provides techniques, which improve this procedure. The main goals of the SA are: i) verification whether a model simulates the phenomenon under study in a proper way (according to physical laws), ii) determination of the model parameters which the most contribute to the model outputs variations, iii) identification the parameters which are not significant for the analysed model outputs, determination the parameters domain of the highest influence of the model variations, iv) estimation of parameters uncertainty, v) verification whether parameters interact with each other. SA will be performed for the model in the project and the results will be used for the model identification.

Experimental data will be supplied by the subcontractor. Dilatometric tests and physical simulations of thermal cycles involving creation of multiphase microstructures will be performed to supply data for the identification of the model. Different preheating cycles will be applied in experiments to obtain various grain size distributions at the beginning of transformation. Particular emphasis will be put on the bainite transformation, which may result in various form of bainite depending on the cooling cycle. Microstructure will be analysed after each test and histograms of the phase composition will be determined. These data will be used in identification of the stochastic phase transformation models. Inverse algorithm described in [32,27] was adapted to the stochastic objective function, see publication [15] for details. Various metrics for the distance between the histograms were analysed in [15] and Bhattacharyya measure [30] was selected as the most efficient. The objective function developed in the WP4 (as presented in Figure 5) will be used in the optimization procedure. The function will be tested using sensitivity analysis and that showing larger sensitivity to the design variables will be selected for further identification. Optimized coefficients in the conventional model, as well as in the statistical model, will be the main output of the WP6.

WP 5. Development of the Statistically Similar Representative Volume Element (SSRVE) for multiphase materials.

Representative Volume Element is commonly used to reproduce microstructure of the material accounting for several specific features. On the other hand, simulation of the RVE deformation requires long computing times and makes multiscale models less effective. Thus, Statistically Similar Representative Volume Element (SSRVE) proposed in [35] will be used in the present project. Authors of the proposal have an experience in developments of the SSRVE for multiphase microstructures. Primary results for dual phase (DP) steels are described in [2]. Construction of the SSRVE requires that the second phase in the material occurs in the form of islands, which are separated one from another. DP steel microstructures composed of soft ferrite (70-80%) and hard martensite (20-30%) meet this requirement. Thus, only measures characterising the hard martensite islands were considered. The material models of the individual constituents will be known from the nano-hardness measurements. The description of the microstructure is based on statistical consideration of certain features. The basic idea is to replace RVE with arbitrary complex inclusion morphology by a periodic one composed of optimal unit cells, see Figure 6. The shape and volume fraction of the hard constituent islands is determined by optimization of various coefficients, which characterise the microstructure [2]. The objective is to obtain similar values of these coefficients for both RVE and SSRVE.

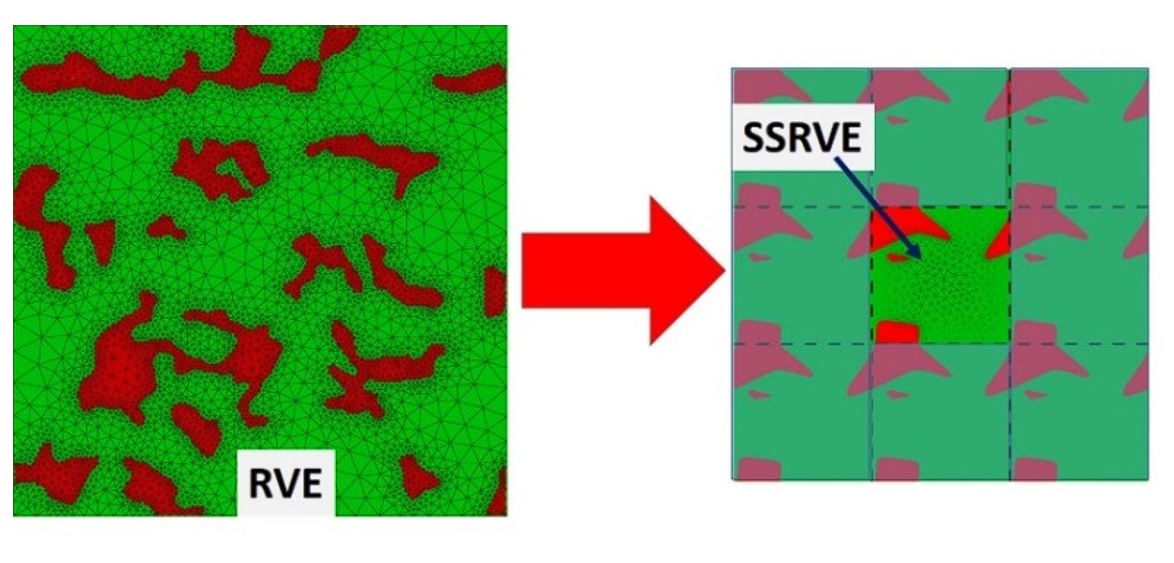
Figure 6 Schematic illustration of the basic concept of the SSRVE, a) RVE, b) periodically arranged SSRVE.

This method was further developed in the project Beethoven [1] for multiphase microstructures characteristic for the DP and CP steels. Additional coefficients, such as length of the boundary between phases, refinement of the hard constituents etc. were added to the objective function, see [16]. In the present project the objective will be extended to reproduce the histograms of the microstructural parameters calculated by the stochastic model will be optimized for each phase separately and SSRVE containing one or two islands of each phase will be developed. Periodic boundary conditions will be applied to represent larger areas of the material. SSRVE method will be used to transform distributions of microstructural parameters calculated by the developed solution of differential equation for stochastic functions into properties and to evaluate this solution, which is the objective of the project.

WP 6. Numerical tests, validation and verification of the model on the basis of experimental data.

Comparison of results obtained from the single point statistical models with experimental data, which were not used in the identification stage, will be the next goal of this WP. Physical and numerical simulation of various thermal cycles during cooling will be performed and the results in the form of histograms will be compared. The methods proposed in the WP 4 will be used to measure the distance between the two results given in the form of stochastic functions. It was observed that the microstructure of bainite in multiphase steels has dominant influence on properties. Therefore, selected bainite microstructure features will be used in the comparison. The microstructure of the bainite can be defined on two different levels: the basic structure, which can be observed by light optical microscopy (LOM) and the sub structure, which can be observed through equipment with higher magnification. The 2nd phase in bainite has different types and forms, which influence the mechanical properties of bainite. These parameters of the bainite microstructure will be obtained from both experiment and simulation in the form of distribution functions. Measurement of the distance between the two sets of results will be again based on the methods proposed in the WP 4. Experimental data will be supplied by the subcontractor.

WP 7. Application of the stochastic model to predict properties of products and to design the optimal process parameters.

This WP is connected with the first example of the application of the model. Having phase transformation model with stochastic variables, we should be able to supply data for the design of the SSRVE following procedure developed in the WP5. Multiscale simulations of two industrial processes will be performed. The first will be laminar cooling after hot rolling and the second will be continuous annealing. FE simulation of deformation of the SSRVEs will be performed and descriptors of the microstructure based on gradients of properties will be calculated. In consequence, correlation between industrial process parameters and product properties will be determined.

Presented approach will allow performing computationally efficient simulations of various cooling schedules. Therefore, we should be able to test an influence of various process parameters on the final product, using them as control parameters in optimization. If successful, by controlling process parameters we should be able to obtain a product with assigned target through the required distribution of properties. Various target microstructures will be proposed in correlation with the require product properties. Process parameters (thermal cycles) will be the design variables.

Using standard approach such as optimization it is hardly possible, since calculation of one iteration can take a few hours or even days, depending on accuracy and complexity of the model. Hence, our last objective is an investigation of possible applications of the model to the design of optimal multiphase microstructures. The Authors have experience in application of the optimization methods [31] to design of metal forming processes [28] and in the inverse analysis for deterministic [32] and stochastic [15] models.

WP 8. Application of the developed stochastic model to reproduce the noisy measurements and to prediction of the uncertainty of the product properties

Modern industry implements various systems of production processes monitoring and data gathering, which work in real time as well as in buffered offline mode. The gathered data are usually introduced to numerical models based on fast artificial intelligence approaches or deterministic computationally intensive algorithms. Nowadays, the models are mainly used for specific purposes focused on predictive maintenance for forecasting of devices lifetime, case based reasoning and assessment of the quality of manufactured elements. The latter application is the most demanding especially in case where non-destructive quality assessment is required to be done in continuous way, while the monitoring of the process parameters is usually very unstable and the measurements are disturbed and noisy. Due to uncertainty of measurements in the industrial processes uncertainty propagation plays a pivotal role in modelling of industrial processes. In such a demanding case classical deterministic models have to be replaced by stochastic approaches. In this project we propose application of the developed stochastic model. Contrary to the application described in the WP 7, in the current solution the unstable process parameters will be assumed to reproduce the disturbed and noisy measurements by the sensors. We collaborate closely with industrial partners, who will supply realistic data concerning uncertainty of temperature measurements. The process of intercritical annealing of multiphase steels will be considered. In this process the material is subjected to a complex thermal cycle and the final product properties depend on phase transformations and are sensitive to the temperature variations. Monte Carlo method will be used to solve evolution equation. This solution will predict properties of product with certain probability accounting for the uncertainty of the process parameters.

4. Research Methodology

Since we have to reveal distribution functions that can generate histograms (initial data), we will consider several different candidates such as skew normal distribution, kernel method distributions etc. For optimization we will consider several distance functions such as Kullback–Leibler divergence, Prohorov metric and others. These tools should allow us to find most appropriate form of equation (6).

Random phenomena during phase transformation, in particular process of nucleation, will be analysed and the idea of the stochastic model will be formulated. The algorithm of the model will be designed and computer program will be written. Following this, sensitivity analysis will be performed and an importance of various coefficients in the model will be estimated. Inverse analysis for the experimental data will be used to determine coefficients in the stochastic model. Dilatometric tests and physical simulations of thermal cycles will be performed to supply information on transformation mechanisms in the investigated steel. The objective function in the inverse analysis will be based on the distance between measured and calculated histograms of selected parameters of the microstructure. Validated model with optimal coefficients will be used to simulate various industrial processes and histograms of microstructural parameters will be calculated. To find the correlation between these histograms and mechanical properties, Statistically Similar Representative Element SSRVE) will be designed. Distribution of microstructural parameters will be implements in the objective function for the SSRVE construction. Prediction of the properties using SSRVE will allow formulating optimization task in the reconstruction problem. The technological parameters, which will allow obtaining required properties, will be calculated. Nature inspired optimization methods will be used.

In the final stage of the project developed stochastic model will be used to predict uncertainty of the properties of product caused by the uncertainty of the input from sensors in the industrial line. 

5. References.

1  Bleck W., Pietrzyk M., Chang Y., Szeliga D., Madej Ł., Haase C, Rauch Ł., Distribution functions for the description of heterogeneous metallic microstructures, Beethoven project financed by DFG in Germany (BL 402/46-1) and NCN in Poland (2016/23/G/ST5/04059), 2018-2021.

2  Rauch Ł., Pernach M., Bzowski K., Pietrzyk M., On application of shape coefficients to creation of the statistically similar representative element of DP steels, Computer Methods in Materials Science, 11, 2011, 531-541.

3  Pietrzyk M., Czyżewska N., Klimczak K., Kusiak J., Morkisz P., Oprocha P., Przybyłowicz P., Rauch Ł., Szeliga D., Stochastic approach to modelling microstructure evolution and properties of metals subjected to thermomechanical processing, NCN project no. 2017/25/B/ST8/01823, 2018-2021.

4 Chang Y., Lin M., Hangen U., Richter S., Haase C., Bleck W., Revealing the relation between microstructural heterogeneities and local mechanical properties of complex-phase steel by correlative electron microscopy and nanoindentation characterization, Materials & Design, 203, 2021, 109620.

5  Heibel S., Dettinger, T., Nester, W., Clausmeyer, T., Tekkaya, A.E., Damage mechanisms and mechanical properties of high-strength multi-phase steels, Materials, 11, 2018, 761.

6  Chang Y., Haase C., Szeliga D., Madej Ł., Hangen U., Pietrzyk M., Bleck W., Compositional heterogeneity in multiphase steels: characterization and influence on local properties, Materials Science and Engineering A, 827, 2021, 142078.

7  Szeliga D., Chang Y., Bleck W., Pietrzyk M., Evaluation of using distribution functions for mean field modelling of multiphase steels, Procedia Manufacturing, 27, 2019, 72-77.

8  Zhang L., Ren W., Samanta A., Du Q., Recent developments in computational modelling of nucleation in phase transformations, Computational Materials, 2, 2016, 16003.

9  Pietrzyk M., Madej Ł., Rauch Ł., Szeliga D., Computational Materials Engineering: Achieving high accuracy and efficiency in metals processing simulations, Elsevier, Amsterdam, 2015.

10  Izmailov, A. F.; Myerson, A. S.; Arnold, S. A statistical understanding of nucleation, Journal of Crystal Growth, 1999, 196, 234−242.

11  Tomellini M., Politi S., Kinetics of phase transformations with heterogeneous correlated-nucleation, Physica A: Statistical Mechanics and its Applications, 513, 2019, 175-188.

12  Maggioni G.M., Mazzotti M., Modelling the stochastic behaviour of primary nucleation, Faraday Discussions, 179, 2015, 359-382.

13  Mecking H., Kocks, U.F., Kinetics of flow and strain-hardening, Acta Metallurgica, 29, 1981, 1865-1875.

14  Estrin Y., Mecking H., A unified phenomenological description of work hardening and creep based on one-parameter models, Acta Metallurgica, 32, 1984, 57-70.

15  Klimczak K., Oprocha P., Kusiak J., Szeliga D., Morkisz P., Przybyłowicz P., Czyżewska N., Pietrzyk M., Inverse problem in stochastic approach to modelling of microstructural parameters in metallic materials during processing, 2021 (submitted to Mathematical Problems in Engineering).

16  Szeliga D., Chang Y., Madej Ł., Bzowski K., Haase C., Bleck W., Pietrzyk M., Correlating the compositional and microstructural heterogeneity and local formability of cold-rolled DP and CP steels through hardness gradient, Steel Research International, to be submitted.

17  Leblond J.B., Devaux J., A new kinetic model for anisothermal metallurgical transformations in steel including effect of austenite grain size, Acta Metallurgica, 32, 1984, 137-146.

18  Milenin I., Pernach M., Pietrzyk M., Application of the control theory for modelling austenite-ferrite phase transformation in steels, Computer Methods in Materials Science, 15, 2015, 327-335.

19 Arnold L., Random dynamical systems, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 1998.

20  Han X., Kloeden P.E., Random ordinary differential equations and their numerical solution, Springer Nature Singapore Pte Ltd., 2017.

21  Soong T.T., Random differential equations in science and engineering, Academic Press, 1973.

22  Khromov K.Y., Soisson F., Stroev A.Y., Vaks V.G., Stochastic statistical theory of nucleation and evolution of nano-sized precipitates in alloys with application to precipitation of copper in iron, Journal of Experimental and Theoretical Physics, 112, 2011, 414–440.

23  Clouet E., Modeling of nucleation processes, in: ASM Handbook Vol. 22A, Fundamentals of modeling for metals processing, Furrer D.U., Semiatin S.L., (Eds.), 2009, 203-219.

24  Cahn J.W., Phase separation by spinodal decomposition in isotropic systems, The Journal of Chemical Physics, 42, 1965, 93-99.

25  Tomellini M., Fanfoni M., Comparative study of approaches based on the differential critical region and correlation functions in modeling phase-transformation kinetics, Physical Review E 90, 2014, 052406.

26  Jentzen A., Kloeden P.E., Pathwise Taylor schemes for random ordinary differential equations, BIT, 49(1), 2009, 113–140.

27 Szeliga D., Gawąd J., Pietrzyk M., Inverse analysis for identification of rheological and friction models in metal forming, Computer Methods in Applied Mechanics and Engineering, 195, 2006, 6778-6798.

28  Kusiak J., Thompson E.G., Optimization techniques for extrusion die shape design, Proc. 3rd Int. Conf. NUMIFORM'89, eds, Thompson E.G., Wood R., Zienkiewicz O.C., Samuelsson A., Fort Collins, 1989, 569-574.

29 Bhattacharyya A.,  On  a  measure  of  divergence  between  two  multinomial  populations,  The Indian Journal of Statistics, 7, 1946, 401–406, doi:10.1038/157869b0.

30  Cha S.-H., Srihari S.N., On measuring the distance between histograms, Pattern Recognition, 35, 2002, 1355-1370.

31  Kusiak J., Danielewska–Tułecka A., Oprocha P., Optymalizacja: wybrane metody z przykładami zastosowań. PWN, 2009.

32  Szeliga D., Identification problems in metal forming: A comprehensive study, publ. AGH University of Science and Technology, no. 291, Krakow, 2013.

33  Salehghaffari S., Rais-Rohani M., Marin E.B., Bammann D.J., A new approach for determination of material constants of internal state variable based plasticity models and their uncertainty quantification, Computational Materials Science, 55, 2012, 237–244. [22B]

34  Czyżewska N., Kusiak J, Morkisz P., Oprocha P., Pietrzyk M., Przybyłowicz P., Rauch Ł., Szeliga, D., On mathematical aspects of evolution of dislocation density in metallic materials, 2020, preprint  arXiv:2011.08504.

35  Schroeder J., Balzani D., Brands S., Approximation of random microstructures by periodic statistically similar representative volume elements based on lineal-path functions, Archives of Applied Mechanics, 81, 2011, 975-997.